抗锯齿
锯齿
锯齿就是采样瑕疵。
走样:锯齿
反走样:抗锯齿
采样瑕疵的表现
1.锯齿

2.摩尔纹

3.车轮效应

瑕疵产生的原因
信号变化的太快,采样太慢
反走样的步骤
先将图像进行模糊,再进行采样
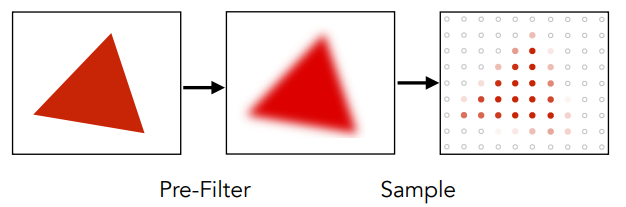
不能先采样,再模糊

频域
频域是描述信号在频率方面特性时用到的一种坐标系。
自变量是频率,即横轴是频率,纵轴是频率信号的幅度,即通常说的频谱图。
傅里叶级数与傅里叶变换
任意周期函数都可以用正弦函数和余弦函数构成的无穷级数来表示。
下图分别是频率为1和频率为2的时域图像
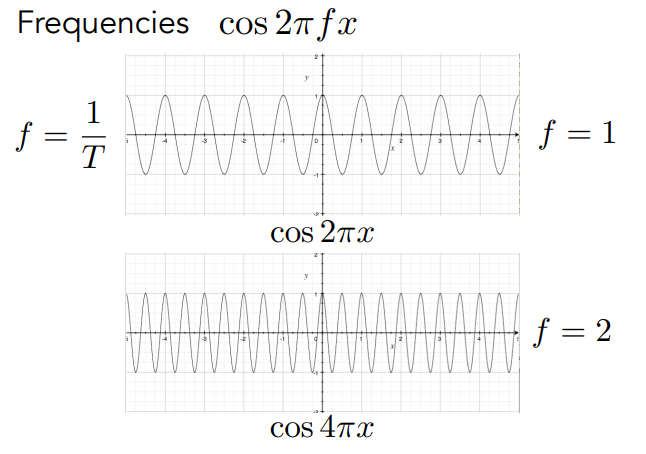
傅里叶变换:将函数从时域转换到频域
逆傅里叶变换:将函数从频域转换到时域

图像的频域
将图像从时域变换到频域后,会形成一张衍射图
其中低频部分集中在图像正中间,而高频部分分布在周围,且离图像中心越远,频率越高。
可以将图形的频率理解为图像颜色变换的剧烈程度,越剧烈,即颜色变化越大,频率越高;越平缓,即颜色相近,频率越低。
低频决定轮廓,高频决定细节。

高通滤波
除去低频部分,只保留高频,即只保留图片中颜色变化大的部分,也就是物体的轮廓

低通滤波
除去高频部分,只保留低频,即只保留图片中颜色变化小的部分,也就是是物体轮廓的颜色变化变得不剧烈,也就是模糊了物体边缘。

卷积
图像卷积
卷积核:一个小的矩阵
卷积就是将卷积核放在图像中,然后将卷积核所覆盖的像素颜色值乘以卷积核中的数值,即权重,然后将得到的数值相加,再进行归一化(平均),就能得到该像素经过卷积后的图像。
卷积实际就是将一个像素对周围的像素求平均,而卷积核就是具体用何种算法进行求平均。
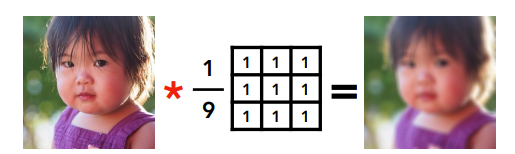
常见的卷积核有矩形卷积核、线性卷积核、B样条卷积核、高斯卷积核等
卷积的时域
时域上的卷积就是频域上的乘积
将卷积核进行傅里叶变换转换到时域图像可以发现,图像中大部分都是低频信号。将图形在时域上进行卷积其实就是在频域上进行低通滤波,所以卷积核也就是低通滤波器。

卷积核面积越大,其求平均时所平均的像素就越多,所以图像越模糊,也就是图像频域保留的高频信号越少,所以可得卷积核的频域面积越小。


反走样
走样原因
采样频率太慢,跟不上频率
从频率角度定义:不同的频率在采样后的频率可能相同,无法区别出采样相同的不同频率
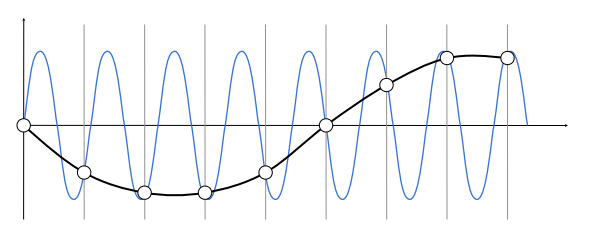
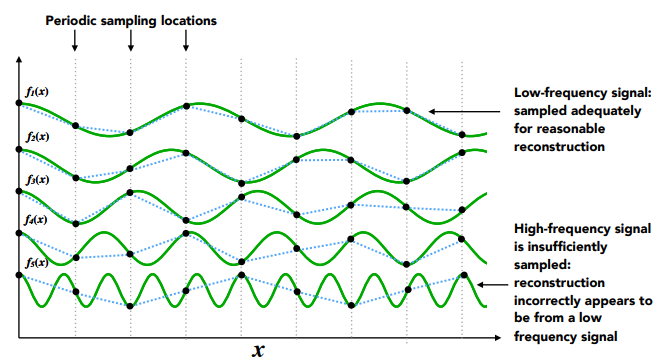
在将采样转换回图像时,原本的高频信号会被识别成低频信号,也就是放大了低频信号,这里称为混叠。(上图中的中高频的f5在采样后变成了低频(蓝色虚线))
锯齿产生的原因:
1.三角形边缘的频率很高,但是采样频率(近似为分辨率)过低,无法采集该高频率信号,并将其识别为了低频信号
2.部分白色被识别成了红色,部分红色被识别成了白色。
反走样
在低采样频率时,无法采样高频信号,而且高频信号会被识别成低频信号从而造成混叠。所以可以在进行采样前将高频信号去除,然后再采样。
就相当于让三角形的边缘不再那么锐利,从而使得采样时能够正确处理三角形边缘。
在去除高频信号时,就要用到上面的低通滤波器。
上文提到不能先采样,再模糊,是因为采样部分采集了高频信号并转化成了低频信号,再进行模糊也无法消除混叠产生的锯齿。
其他反走样方法
MSAA
通过超级采样进行抗锯齿
将一个像素分为多个像素,求出每个子像素的颜色后进行平均,得到该像素的颜色值。
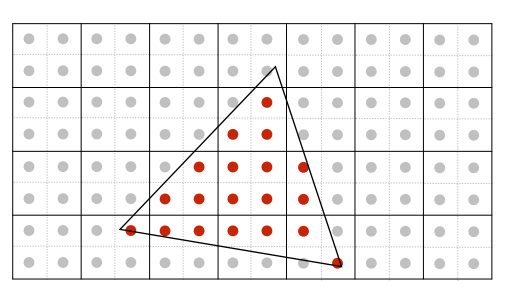
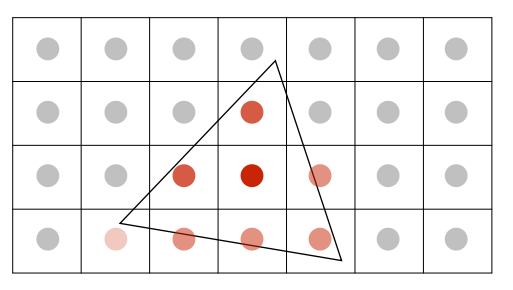
这样会导致计算量的大量增加。
工业上通常不会用规整图形来划分像素,并且像素相邻部分的子像素会为复用以降低计算量。
FXAA
在采样阶段不进行任何抗锯齿的操作,而在画面生成结束后用固定的模版匹配画面中的锯齿,然后将锯齿像素替换掉。
该算法速度快,计算量小,但是部分场景下效果不好。
TAA
分析前面多帧的画面,计算像素的平均颜色。
深度测试
画家算法
先光栅化远处的物体,再画近处的物体。先画模型的远处的面,再画近处的面。
但无法处理以下图形:
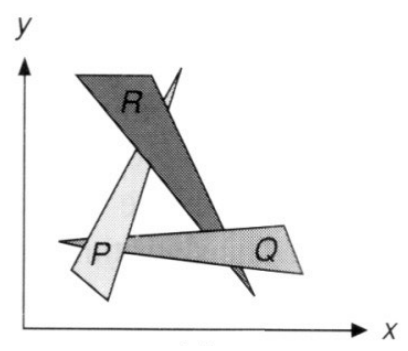
深度缓存
生成画面时,同时生成帧缓冲和深度缓存,帧缓冲记录每个像素的颜色,深度缓存记录每个像素的最浅深度信息。
由于经过视图变换后,相机处于原点,看向-Z方向。可以将模型的Z坐标看做是深度,即距离相机的距离,距离越小越近。

for (each triangle T)
for (each sample (x,y,z) in T)
if (z < zbuffer[x,y]) // closest sample so far
framebuffer[x,y] = rgb; // update color
zbuffer[x,y] = z; // update depth
else
; // do nothing, this sample is occluded