模版

//用a表示原数组originalArray，用p表示前缀和prefixSum,用d表示差分difference
//一维前缀
a[0]=p[0]=0;
p[i]=a[i]+p[i-1];   //生成前缀和
a[i]=p[i]-p[i-1];   //还原原数组
sum=p[r]-p[l-1];   //求区间l-r的和
//一维差分
a[0]=d[0]=0;
d[i]=a[i]-a[i-1];   //生成差分数组
a[i]=a[i-1]+d[i];   //还原原数组
d[l]+=c;   //将区间l-r中的每个元素加c
d[r+1]-=c;

//二维前缀和
p[i][j]=a[i][j]+p[i-1][j]+p[i][j-1]-p[i-1][j-1];   //生成前缀和
a[i][j]=p[i][j]-p[i-1][j]-p[i][j-1]+p[i-1][j-1];   //还原原数组
sum=p[x2][y2]-p[x1-1][y2]-p[x2][y1-1]+p[x1-1][y1-1];   //求区间(x1,y1)-(x2,y2)的和
//二维差分
d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];   //生成差分数组
a[i][j]=d[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1];   //还原原数组
d[x1][y1]+=c;   //将区间(x1,y1)-(x2,y2)的加c
d[x2+1][y1]-=c;
d[x1][y2+1]-=c;
d[x2+1][y2+1]+=c;   

//三维前缀和
p[x][y][z]=a[x][y][z]+p[x-1][y][z]+p[x][y-1][z]+p[x][y][z-1]-p[x-1][y-1][z]-p[x-1][y][z-1]-p[x][y-1][z-1]+p[x-1][y-1][z-1];   //生成前缀和
a[x][y][z]=p[x][y][z]-p[x-1][y][z]-p[x][y-1][z]-p[x][y][z-1]+p[x-1][y-1][z]+p[x-1][y][z-1]+p[x][y-1][z-1]-p[x-1][y-1][z-1];
   //还原原数组
sum=p[x2][y2][z2]-p[x1-1][y2][z2]-p[x2][y1-1][z2]-p[x2][y2][z1-1]+p[x1-1][y1-1][z2]+p[x1-1][y2][z1-1]+p[x2][y1-1][z1-1]-p[x1-1][y1-1][z1-1];   //求区间(x1,y1,z1)-(x2,y2,z2)的和
//三维差分
d[x][y][z]=a[x][y][z]-a[x-1][y][z]-a[x][y-1][z]-a[x][y][z-1]+a[x-1][y-1][z]+a[x-1][y][z-1]+a[x][y-1][z-1]-a[x-1][y-1][z-1];   //生成差分数组
a[x][y][z]=d[x][y][z]+a[x-1][y][z]+a[x][y-1][z]+a[x][y][z-1]-a[x-1][y-1][z]-a[x-1][y][z-1]-a[x][y-1][z-1]+a[x-1][y-1][z-1];   //还原原数组
d[x1][y1][z1]+=c;
   //将区间(x1,y1,z1)-(x2,y2,z2)中的每一个元素加c
d[x2+1][y1][z1]-=c;
d[x1][y1][z2+1]-=c;
d[x2+1][y1][z2+1]+=c;
d[x1][y2+1][z1]-=c;
d[x2+1][y2+1][z1]+=c;
d[x1][y2+1][z2+1]+=c;
d[x2+1][y2+1][z2+1]-=c;

一维

前缀和

前缀和是数组的每一个元素都是元素的原数据加上前面的所有元素的和。可以用来求区间和。

原数组：	1	2	3	4	5	6
前缀和：	1	3	6	10	15	21

前缀和数组记录的是当前元素以及前面所有的元素的信息。
一般在生成前缀和时下标都从1开始，并定义originalArray[0]=prefixSum[0]=0;

a[0]=p[0]=0;
p[i]=a[i]+p[i-1];   //生成前缀和
a[i]=p[i]-p[i-1];   //还原原数组
sum=p[r]-p[l-1];   //求区间l-r的和

差分

差分指的是变化量，差分数组记录的是当前元素和前面一个元素的差值。可以用来快速的对一个区间的元素统一加、减一个数，而不必依次修改区间的每一个数。

原数组：	1	3	5	2	4	6
差分数组：	1	2	2	-3	2	2

差分数组的每一个元素只记录了当前元素和前面元素的关系，并不携带前面所有元素的信息。同样下标默认从1开始，并定义originalArray[0]=difference[0]=0;

a[0]=d[0]=0;
d[i]=a[i]-a[i-1];   //生成差分数组
a[i]=a[i-1]+d[i];   //还原原数组
d[l]+=c;   //将区间l-r中的每个元素加c
d[r+1]-=c;

观察公式发现，还原原数组的过程就是对差分数组求前缀和。
在修改区间的时候，将difference[l]加a即改变了l元素与l-1元素的差，但是后面元素的差分不变，所以l后面的数都会被加a，difference[r+1]减a，即改变了r+1元素与r元素的差，把原本增加数再减去，使得r后面的数先加a再减a，即不变。这样就做到了修改区间l-r的数。

二维

前缀和

与一维前缀和一样，二维前缀和是当前元素和前面所有元素的和。这里的前面所有元素指的是从(0,0)到(i,j)这两点所形成的矩形区域。

在计算前缀和时，不会将当前元素依次与前面每一个元素相加，而是利用前面计算好的前缀和，再加上当前元素。

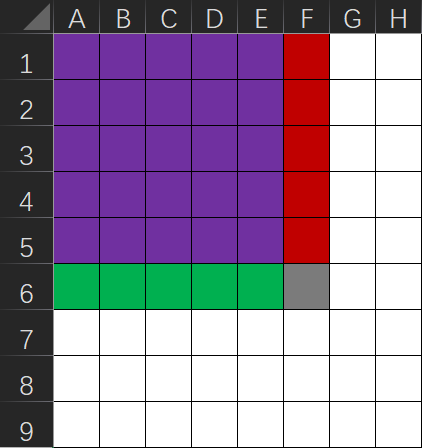
如图，用每一个格子表示一个元素，下标从(1,1)开始。令行为i，列为j。如果想要求(6,F)位置的前缀和，如果将(6,F)与(6,E)的前缀和相加（灰色，绿色与紫色区域），则会漏掉第F列的数据(红色区域)。同理，(6,F)与(5,F)的前缀和相加（灰色，红色与紫色区域），则会漏掉第6行的数据（绿色区域）。所以同时将(6,F)与(6,E)(5,F)的前缀和相加，就不会有遗漏的元素，但是这时(5,E)的前缀和（紫色区域）会被重复计算，所以需要再减一次(5,E)的前缀和。

同样，在根据前缀和还原原数组的时候，将(6,F)的前缀和减去(6,E)(5,F)的前缀和时，(5,E)的前缀和（紫色区域）会被重复减去，所以要再加一次(5,E)的前缀和。

p[i][j]=a[i][j]+p[i-1][j]+p[i][j-1]-p[i-1][j-1];   //生成前缀和
a[i][j]=p[i][j]-p[i-1][j]-p[i][j-1]+p[i-1][j-1];   //还原原数组

如图，在利用前缀和求(5,D)到(6,F)这个区间的和时，可以用(6-F)的前缀和减去(6,C)（绿色与紫色区域）与(4,F)（红色与紫色区域）的前缀和，但同时(4,C)的前缀和（紫色区域）被减去的了两次，所以要再加一次(4,C)的前缀和

sum=p[x2][y2]-p[x1-1][y2]-p[x2][y1-1]+p[x1-1][y1-1];   //求区间(x1,y1)-(x2,y2)的和

差分

在一维差分中，还原原数组的过程就是对差分数组求前缀和。
同样可以得出，二维差分中，还原原数组的过程就是对二维差分数组求前缀和，即原数组=差分数组的前缀和：a[i][j]=d[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1];
变形公式可得：

d[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1];   //生成差分数组
a[i][j]=d[i][j]+a[i-1][j]+a[i][j-1]-a[i-1][j-1];   //还原原数组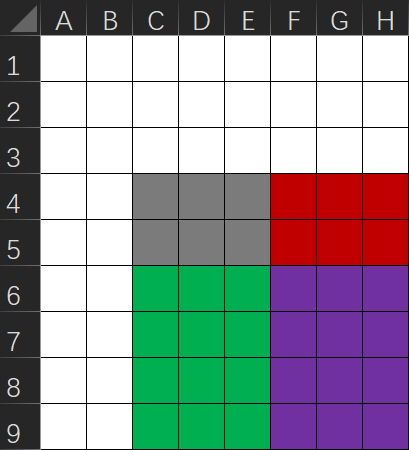

如图，在修改二维差分数组中的一个元素时，如(4,C)，会导致(4,C)及后面的所有元素都被改变（灰色、红色、绿色、紫色区域）。所以想要仅修改灰色区域的数据（加a），可以将(4,C)加a，然后将(4,F)的差分（红色和紫色区域）和(6,C)的差分（绿色和紫色的区域）减a，来抵消(4,C)加a造成的数值改变，但是会导致(6,F)后面区域的数值（紫色区域）被减了两次a，所以需要将(6,F)的差分再加一次a。

d[x1][y1]+=c;   //将区间(x1,y1)-(x2,y2)的加c
d[x2+1][y1]-=c;
d[x1][y2+1]-=c;
d[x2+1][y2+1]+=c;   

三维

前缀和

p[x][y][z]=a[x][y][z]+p[x-1][y][z]+p[x][y-1][z]+p[x][y][z-1]-p[x-1][y-1][z]-p[x-1][y][z-1]-p[x][y-1][z-1]+p[x-1][y-1][z-1];   //生成前缀和
a[x][y][z]=p[x][y][z]-p[x-1][y][z]-p[x][y-1][z]-p[x][y][z-1]+p[x-1][y-1][z]+p[x-1][y][z-1]+p[x][y-1][z-1]-p[x-1][y-1][z-1];
   //还原原数组
sum=p[x2][y2][z2]-p[x1-1][y2][z2]-p[x2][y1-1][z2]-p[x2][y2][z1-1]+p[x1-1][y1-1][z2]+p[x1-1][y2][z1-1]+p[x2][y1-1][z1-1]-p[x1-1][y1-1][z1-1];   //求区间(x1,y1,z1)-(x2,y2,z2)的和

差分

和二维差分一样，利用原数组=差分数组的前缀和求出三维差分的公式。
a[x][y][z]=d[x][y][z]+a[x-1][y][z]+a[x][y-1][z]+a[x][y][z-1]-a[x-1][y-1][z]-a[x-1][y][z-1]-a[x][y-1][z-1]+a[x-1][y-1][z-1];
变形后得：

d[x][y][z]=a[x][y][z]-a[x-1][y][z]-a[x][y-1][z]-a[x][y][z-1]+a[x-1][y-1][z]+a[x-1][y][z-1]+a[x][y-1][z-1]-a[x-1][y-1][z-1];   //生成差分数组
a[x][y][z]=d[x][y][z]+a[x-1][y][z]+a[x][y-1][z]+a[x][y][z-1]-a[x-1][y-1][z]-a[x-1][y][z-1]-a[x][y-1][z-1]+a[x-1][y-1][z-1];   //还原原数组
d[x1][y1][z1]+=c;
   //将区间(x1,y1,z1)-(x2,y2,z2)中的每一个元素加c
d[x2+1][y1][z1]-=c;
d[x1][y1][z2+1]-=c;
d[x2+1][y1][z2+1]+=c;
d[x1][y2+1][z1]-=c;
d[x2+1][y2+1][z1]+=c;
d[x1][y2+1][z2+1]+=c;
d[x2+1][y2+1][z2+1]-=c;