范数
L1范数
L1范数是向量中所有元素绝对值的和。对于一个向量 $ w = [w_1, w_2, …, w_n] $,其L1范数定义为:
$$
|w|_1 = |w_1| + |w_2| + … + |w_n|
$$
L1范数常用于稀疏性约束,因为它会促使某些权重变为零,从而实现特征选择。
L2范数
L2范数是向量中所有元素平方和的平方根。对于同一个向量 $w$,其L2范数定义为:
$$
|w|_2 = \sqrt{w_1^2 + w_2^2 + … + w_n^2}
$$
在机器学习中,L2范数通常用于正则化,以防止模型过拟合。在权重衰减中,L2范数惩罚项可以限制权重参数的大小,使它们接近于零。
方法
权重衰减等价于 $L_2$ 范数正则化(regularization)。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小,是应对过拟合的常用手段。具体来说,权重衰减通过在损失函数中加入一个与权重参数的L2范数成正比的惩罚项,来限制模型权重的增长。
$L_2$范数正则化在模型原损失函数基础上添加$L_2$范数惩罚项,从而得到训练所需要最小化的函数。$L_2$范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。以3.1节(线性回归)中的线性回归损失函数
$$
\ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b – y^{(i)}\right)^2
$$
为例,其中$w_1, w_2$是权重参数,$b$是偏差参数,样本$i$的输入为$x_1^{(i)}, x_2^{(i)}$,标签为$y^{(i)}$,样本数为$n$。将权重参数用向量$\boldsymbol{w} = [w_1, w_2]$表示,带有$L_2$范数惩罚项的新损失函数为
$$
\ell(w_1, w_2, b) + \frac{\lambda}{2n} |\boldsymbol{w}|^2,
$$
其中超参数$\lambda > 0$。当权重参数均为0时,惩罚项最小。当$\lambda$较大时,惩罚项在损失函数中的比重较大,这通常会使学到的权重参数的元素较接近0。当$\lambda$设为0时,惩罚项完全不起作用。上式中$L_2$范数平方$|\boldsymbol{w}|^2$展开后得到$w_1^2 + w_2^2$。有了$L_2$范数惩罚项后,在小批量随机梯度下降中,将线性回归一节中权重$w_1$和$w_2$的迭代方式更改为
$$
\begin{aligned}
w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 – \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b – y^{(i)}\right),\\
w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 – \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b – y^{(i)}\right).
\end{aligned}
$$
可见,$L_2$范数正则化令权重$w_1$和$w_2$先自乘小于1的数,再减去不含惩罚项的梯度。因此,$L_2$范数正则化又叫权重衰减。权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制,这可能对过拟合有效。实际场景中,有时也在惩罚项中添加偏差元素的平方和。
L2范数正则化如何应对过拟合?
限制模型复杂度
模型的复杂度通常与权重参数的大小相关。较大的权重参数可能导致模型对训练数据中的微小变化过于敏感,从而拟合噪声。L2正则化通过约束权重参数的大小,降低了模型的复杂度,使其更倾向于学习数据的整体趋势,而不是噪声或异常点。
平滑决策边界
在分类任务中,较大的权重参数可能导致决策边界非常陡峭或复杂。这种复杂的决策边界容易导致过拟合,因为它们可能会将训练数据中的噪声误认为是重要的特征。L2正则化通过缩小权重参数,使得决策边界更加平滑,从而提高模型的泛化能力。
减少极端权重的影响
在深度学习或高维数据中,某些特征可能具有极大的权重值,这会导致模型对这些特征的变化过于敏感。L2正则化通过惩罚大权重值,减少了这些极端权重对模型的影响,从而使模型更加鲁棒。
高维线性回归实验
设数据样本特征的维度为$p$。对于训练数据集和测试数据集中特征为$x_1, x_2, \ldots, x_p$的任一样本,使用如下的线性函数来生成该样本的标签:
$$
y = 0.05 + \sum_{i = 1}^p 0.01x_i + \epsilon
$$
其中噪声项$\epsilon$服从均值为0、标准差为0.01的正态分布。为了较容易地观察过拟合,考虑高维线性回归问题,如设维度$p=200$;同时,特意把训练数据集的样本数设低,如20。
import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt
from IPython import display
n_train, n_test, num_inputs = 20, 100, 200
true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05 # torch.ones 是生成一个全为1的张量
features = torch.randn((n_train + n_test, num_inputs)) # 生成x
labels = torch.matmul(features, true_w) + true_b # 生成y
labels += torch.tensor(np.random.normal(0, 0.01, size=labels.size()), dtype=torch.float) # 加入噪声
train_features, test_features = features[:n_train, :], features[n_train:, :] # 划分训练集和测试集
train_labels, test_labels = labels[:n_train], labels[n_train:] # 划分训练集和测试集从零开始实现
初始化模型参数
def init_params():
w = torch.randn((num_inputs, 1), requires_grad=True) # 生成w,设置梯度
b = torch.zeros(1, requires_grad=True) # 生成b,设置梯度
return [w, b] # 返回w和b3.12.3.2 定义$L_2$范数惩罚项
下面定义$L_2$范数惩罚项。这里只惩罚模型的权重参数。
def l2_penalty(w):
return (w**2).sum() / 2 # 返回l2范数3.12.3.3 定义训练和测试
定义线性模型,损失函数和优化算法
def linreg(X, w, b):
return torch.mm(X, w) + b
def squared_loss(y_hat, y):
# 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2
return ((y_hat - y.view(y_hat.size())) ** 2) / 2
def sgd(params, lr, batch_size):
for param in params:
param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data定义绘图函数
def set_figsize(figsize=(3.5, 2.5)):
display.set_matplotlib_formats('png')
plt.rcParams['figure.figsize'] = figsize
def semilogy(x_vals, y_vals, x_label, y_label, x2_vals=None, y2_vals=None,
legend=None, figsize=(3.5, 2.5)):
set_figsize(figsize)
plt.xlabel(x_label)
plt.ylabel(y_label)
plt.semilogy(x_vals, y_vals) # y轴使用对数尺度
if x2_vals and y2_vals:
plt.semilogy(x2_vals, y2_vals, linestyle=':')
plt.legend(legend)
plt.show()训练模型
batch_size, num_epochs, lr = 1, 100, 0.003 # 设置超参数
net, loss = linreg, squared_loss # 设置模型和损失函数
dataset = torch.utils.data.TensorDataset(train_features, train_labels) # 设置数据集
train_iter = torch.utils.data.DataLoader(dataset, batch_size, shuffle=True) # 设置数据迭代器
def fit_and_plot(lambd):
w, b = init_params() # 初始化参数
train_ls, test_ls = [], [] # 初始化损失
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X, w, b), y) + lambd * l2_penalty(w) # 添加了L2范数惩罚项
l = l.sum() # 损失求和
if w.grad is not None: # 梯度清零
w.grad.data.zero_()
b.grad.data.zero_()
l.backward() # 反向传播
sgd([w, b], lr, batch_size) # 更新参数
train_ls.append(loss(net(train_features, w, b), train_labels).mean().item()) # 计算训练集损失
test_ls.append(loss(net(test_features, w, b), test_labels).mean().item())
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test']) # 画图
print('L2 norm of w:', w.norm().item()) # 输出L2范数观察过拟合
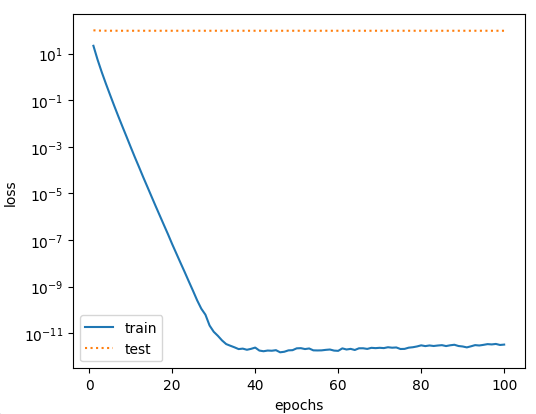
fit_and_plot(lambd=0) # 不使用权重衰减输出:
L2 norm of w: 14.070374488830566结果训练误差远小于测试集上的误差。这是典型的过拟合现象。
使用权重衰减
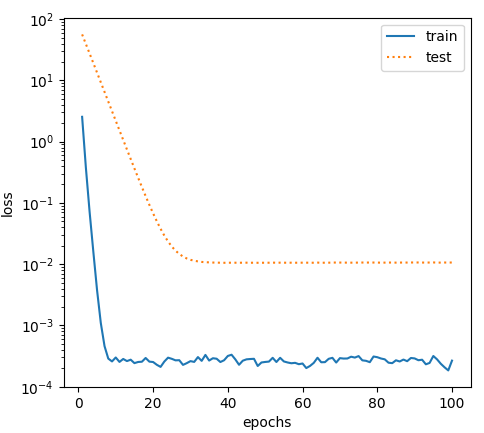
fit_and_plot(lambd=3) # 使用权重衰减输出:
L2 norm of w: 0.033579129725694656训练误差虽然有所提高,但测试集上的误差有所下降。过拟合现象得到一定程度的缓解。另外,权重参数的$L_2$范数比不使用权重衰减时的更小,此时的权重参数更接近0。
简洁实现
直接在构造优化器实例时通过weight_decay参数来指定权重衰减超参数。默认下,PyTorch会对权重和偏差同时衰减。分别对权重和偏差构造优化器实例,从而只对权重衰减。
def fit_and_plot_pytorch(wd):
# 对权重参数衰减。权重名称一般是以weight结尾
net = nn.Linear(num_inputs, 1) # 线性回归模型
nn.init.normal_(net.weight, mean=0, std=1) # 初始化权重
nn.init.normal_(net.bias, mean=0, std=1) # 初始化偏差
optimizer_w = torch.optim.SGD(params=[net.weight], lr=lr, weight_decay=wd) # 对权重参数衰减
optimizer_b = torch.optim.SGD(params=[net.bias], lr=lr) # 不对偏差参数衰减
train_ls, test_ls = [], [] # 初始化损失
for _ in range(num_epochs):
for X, y in train_iter:
l = loss(net(X), y).mean() # 计算损失
optimizer_w.zero_grad() # 梯度清零
optimizer_b.zero_grad() # 梯度清零
l.backward() # 反向传播
# 对两个optimizer实例分别调用step函数,从而分别更新权重和偏差
optimizer_w.step()
optimizer_b.step()
train_ls.append(loss(net(train_features), train_labels).mean().item())
test_ls.append(loss(net(test_features), test_labels).mean().item())
semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',
range(1, num_epochs + 1), test_ls, ['train', 'test'])
print('L2 norm of w:', net.weight.data.norm().item())